With a wife with a masters in education, you tend to think and chat about education from time to time. I enjoy thinking about how social software could help education in the future. One of the fields that I enjoy thinking about is Maths. It was my favorite subject as a kid and I had the benefit of a great teacher. In general though, it feels like Math is often taught in such a painful way.
I remember being sent an article that discussed how Math is taught by comparing it to music. It postulates a world in which music is taught without instruments. You have to learn music theory for 10 years before you get to pick up that flute. What kid would get excited about a world of that music? That is what we do to them with Math.

Time for Pie
I mentioned the Bespin pie menu before. In our first version you jump to the different pieces with the keyboard. Of course, one of the benefits of a pie menu is that Fittss’s Law kicks in and you can easily jump to an item. (Aside: the dirty secret of our pie menu is that it isn’t really a pie menu, it currently sits at the bottom and not where you right click etc.)
As we start to put in mouse support, the first thing we need to do is be able to determine which slice of the pie is being clicked on so we can activate it. This gave me the opportunity to go down trigonometry lane.
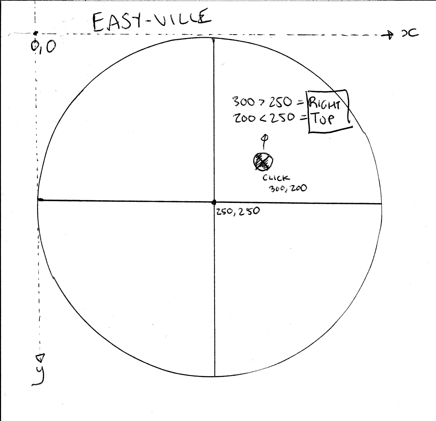
If the pie was sliced with vertical and horizontal lines like the image above, then it would be very simple indeed. To start with, what information do you get when the user clicks? We get an x and y coordinate with an origin starting point in the top left. There are various x and y coordinates that you will get from the MouseEvent (x, y, offsetX/Y, pageX/Y, rangeX/Y, clientX/Y, layerX/Y). We care about the offsetX/Y or layerX/Y value (depending on the browser), which will give us the point with the origin starting at the top left of the canvas itself and not the window.
With the example above you could simply take the computed x and y coordinates and simply check them to determine the segment. For example, if x is less than the radius then it is a segment on the left. If y is less than the radius then it is a segment on top.
But we don’t have that luxury. Instead we have to do some simple Math. I drew out the problem with various bits of information here:
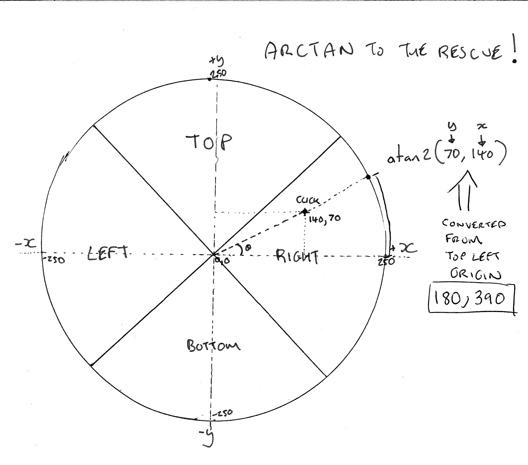
You will see the slices match the pie menu, and I drew in an X and Y axis that cuts through the center of the pie. In the diagram you will see an “x” marking the click in the right slice. How do we work it out? Well, what do we know? First we can calculate the location of the point based on the center of the circle. Remember that the browser will tell you the x and y based on the top left and not the center, so we quickly repurpose the coordinate based on the top left of 390, 180 and convert it to 140, 70. This is simply done via:
function centerPoint(x, y) { return { x: x - RADIUS, y: (y - RADIUS) * -1 }; }
Now we have the relative point from the center of the circle we can calculate the angle that will then in turn let us know which quadrant we are in.
Arctan and atan2()
The easiest way to calculate which quadrant we are in is to simply calculate the angle of the dangle. To do that we calculate the arc tangent between two lines in a triangle, the y=0 line across the x axis, and a line between y=0 and the point in question.
It turns out that we get this calculation for free, via Math.atan2:
function angle(x, y) { return Math.atan2(y, x) * 180 / Math.PI; }
To explain how this works, see the scribble below that shows 4 different points and the resulting angles based on angle(). One gotcha that you will notice is that atan2() takes the coordinates in the order: y, x but elsewhere you are used to using the opposite x and then y. Be careful!
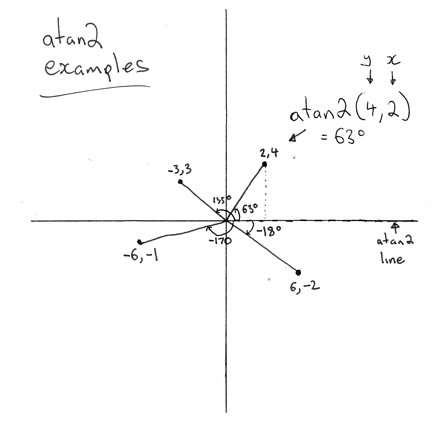
Once we have the angle based on the x axis, we can have a simple case statement to check the bounds.
If the angle is below -45 and 45 degrees, it is on the right. Greater than 45 and less than 135? Then we have the top. And so on.
With a little fun Math, we get to have Pi solve our Pie problem. To see the code at work, check out the test bed.

June 4th, 2009 at 12:10 pm
Using atan2 to solve this seems to be a bit like overkill; a coordinate change (with your easy-ville solution) would probably function better.
June 4th, 2009 at 1:43 pm
Trig is cool but occasionally people resort to it prematurely.
High school linear algebra applies.
You have two lines that each divide the plane in two. One line is y=x and the other line is y=-x. You can compute a boolean for each line that says which side you’re on.
var a = y>-x; var b = !a;
var c = y>x; var d = !c;
If area one is the area that contains (1,0) and you number counter-clockwise,
var area;
if (d & a) area=1;
if (c & a) area = 2;
if (c & b) area = 3;
if (d & b) area = 4;
Optimization left to the reader.
Now suppose you want the wedges that contain (1,0) and (-1,0) to be thinner than the wedges that contain (0,1) and (0,-1). This simply changes the equations of your lines and the resulting definitions of the predicates a, b, c and d.
Suppose the slopes of these lines are .5 and -.5:
y = x *.5;
y = -x *.5;
Change two statements of the code:
var a = y > -x*.5;
var c = y > x*.5;
The rest of the above logic would be the same.
June 4th, 2009 at 1:50 pm
I did something similar a while ago, it’s in dojoc. I used dojox.gfx to draw the pie, and trig to figure out the angle. There’s also some code there so that it can support any number of menu items.
You can grab the code here: http://svn.dojotoolkit.org/dojoc/sandbox/piemenu/
June 4th, 2009 at 3:06 pm
Dion’s general solution works for an arbitrary number of slices. If you want small, incomprehensible and quadrants only, you could also do:
return ["bottom","left","right","top"][(x>y?2:0)+(500-x>y?1:0)];
Needless to say, I’ll leave Dion’s version in Bespin, if only to prevent him from changing the number of slices. ;-)
June 4th, 2009 at 6:21 pm
This is neat if only because I’m finishing my school year learning trigonometric identities. I’ve always wanted to make a circle menu.
June 4th, 2009 at 7:42 pm
Awesome comments!
@Joe Ah come on mate, there is always room for a new slice of pie ;)
@Mike: Great point for this solution!
@zznq: Very true. atan2 is so simple though that it didn’t seem like more work really.
June 7th, 2009 at 12:55 pm
oh yes, I had to solve this on my own some years ago :D
But to put a little bit more math in there: you should calculate the distance between the center of the pie and the mouse-click-point. If this distance > radius => user clicked outside of the pie => we don’t have to care about this ;)
That’s where you bring in the nice math equation: a^2 + b^2 = c^2.
And who wants to miss this nice equation ;)